Skip to main content

R语言心理学网络分析应用

2 基本概念与图论基础

2.1 网络与图的概念

2.1.1 结点与边

网络（或图）1一般由结点和边组成。在心理学的网络分析中，结点（node或vertex）代表网络中的个体或实体，如心理特质、症状、因素、社会个体等等。边（edge）则表示结点之间的关系或连接，如相关性、因果关系、相互作用、社会关系等。

2.1.2 有向图与无向图

有向图（directed graph）中的边具有方向性，表示从一个结点指向另一个结点的关系。例如，微博上的关注关系就是有向的。在心理学的研究中，有时使用有向图来表示变量之间的因果关系。无向图（undirected graph）中的边没有方向性，表示结点之间的双向关系，如微信上的好友关系。很多临床心理学领域的网络分析就使用的是无向图，例如一个由多个变量之间的相关系数构成的网络就是无向图。下图就是一个关注多个临床心理学症状的网络分析的示例2。

A 患者个体的八种症状之间的配对关联；该网络基于时间序列数据，因此是一个有向图。 B 患者群体的八种症状之间的配对关联；该网络基于横断数据，因此是一个无向图。
A 患者个体的八种症状之间的配对关联；该网络基于时间序列数据，因此是一个有向图。 B 患者群体的八种症状之间的配对关联；该网络基于横断数据，因此是一个无向图。

2.1.3 有权图与无权图

有权图（weighted graph）中的边具有权重，表示关系的强度或容量。例如，一个描述各种心理症状关系的网络中的权重可能是症状之间的偏相关系数。无权图（unweighted graph）中的边没有权重，表示关系的存在或不存在。

2.1.4 图的表示：邻接矩阵

邻接矩阵（adjacency matrix）是一种表示图的方法，其中矩阵的行和列对应于图的结点，矩阵中的元素表示结点之间的边。例如，元素 \(A_{ij}\) 表示结点 \(i\) 和结点 \(j\) 之间是否存在边。在有权图中，\(A_{ij}\) 也表示两个结点之间的权重。

例如，一个包括5个结点的网络的邻接矩阵如下：

\[ \begin{bmatrix} 0& 2.5& 0& 0& 7.8\\ 0& 0& 3.1& 0& 0\\ 0& 0& 0& 4.6& 0\\ 0& 0& 0& 0& 5.2\\ 0& 0& 0& 0& 0 \end{bmatrix} \]

可以绘制为这样的一个有向图：

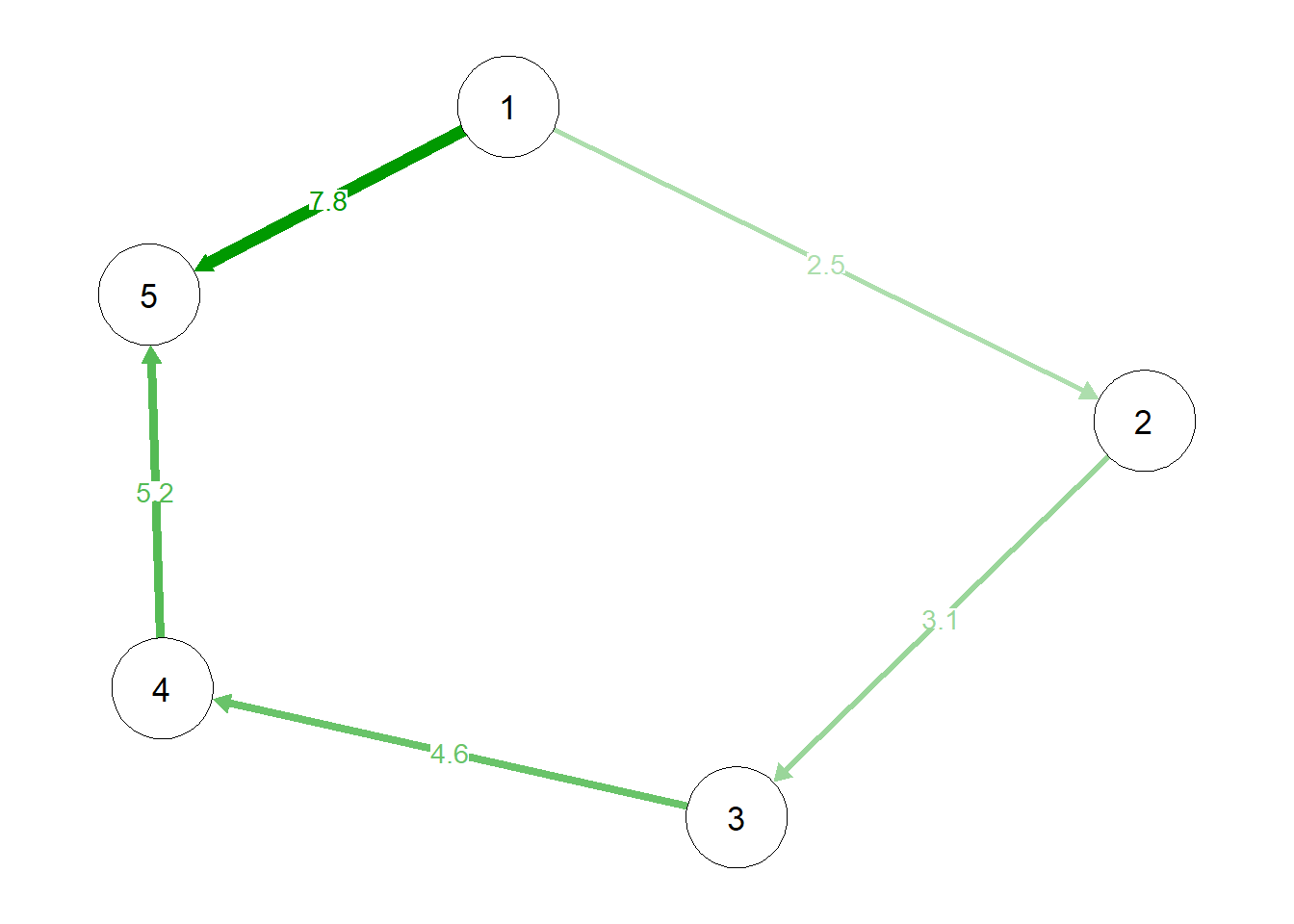
当然我们也会发现，对于刚才的邻接矩阵，矩阵中的大部分元素都是0。这样的稀疏矩阵在存储时效率较低，当结点数量很庞大时会占用大量空间（空间复杂度\(O(n^2)\)）。因此，除了使用邻接矩阵，我们也可以使用邻接表等方法表示一个图。

2.1.5 在igraph里表示一个网络

igraph包是R语言中用于网络分析和图操作的强大工具。它提供了丰富的函数库，支持创建、操作、可视化和分析图结构。这一部分的教程将简单介绍igraph中一些重要的函数和操作。关于igraph的更多详细内容可以阅读该包的帮助文档或者访问igraph主页 https://r.igraph.org/。

library('igraph')
#> 
#> Attaching package: 'igraph'
#> The following objects are masked from 'package:stats':
#> 
#>     decompose, spectrum
#> The following object is masked from 'package:base':
#> 
#>     union

在igraph中，我们可以用一个igraph对象来表示一个网络。一般我们可以通过输入边列表或者邻接矩阵来创建igraph对象，我们也可以使用函数生成特定的随机网络。

2.1.5.1 从边列表创建

创建igraph对象最常用的方法是make_graph，它会根据指定的边构建一个网络。 例如，要创建一个有8个结点（编号为1至8）以及连接结点1-2、2-3、3-4三条边的有向图：

edges <- c(1, 2, 2, 3, 3, 4)
g <- make_graph(edges, n = 8, directed = TRUE)

查看这个网络

g
#> IGRAPH e4008f5 D--- 8 3 -- 
#> + edges from e4008f5:
#> [1] 1->2 2->3 3->4

2.1.5.2 从邻接矩阵创建

另外一种比较常用的创建igraph对象的方法是从邻接矩阵创建。在心理学研究中，邻接矩阵往往相对容易获得，例如我们可以使用各种估计方法（如qgraph中的EBICglasso）获得变量之间的偏相关系数矩阵，这个偏相关系数矩阵就可以作为邻接矩阵创建我们的图。

这个邻接矩阵可以表示无权图：

adjacent_matrix <- matrix(sample(0:1, 100, replace = TRUE, prob = c(0.9, 0.1)), ncol = 10)
g <- graph_from_adjacency_matrix(adjacent_matrix)
g
#> IGRAPH e407cfb D--- 10 12 -- 
#> + edges from e407cfb:
#>  [1]  1-> 5  2-> 1  4-> 4  4-> 9  7-> 5  7-> 7  9-> 1  9-> 4
#>  [9]  9-> 6  9-> 7  9->10 10->10

也可以表示有权图：

adjacent_matrix <- matrix(sample(0:5, 100, replace = TRUE, prob = c(0.9, 0.02, 0.02, 0.02, 0.02, 0.02)), ncol = 10)
g <- graph_from_adjacency_matrix(adjacent_matrix, weighted = TRUE)
g
#> IGRAPH e40b87e D-W- 10 5 -- 
#> + attr: weight (e/n)
#> + edges from e40b87e:
#> [1]  2->2  4->8  6->6  9->7 10->9

2.1.5.3 生成随机网络

igraph为我们提供了一系列生成随机图的方法，这些函数一般以sample开头。例如，我们可以使用sample_smallworld生成一个Watts-Strogatz小世界网络。

g <- sample_smallworld(1, 50, 5, 0.05)
plot(g)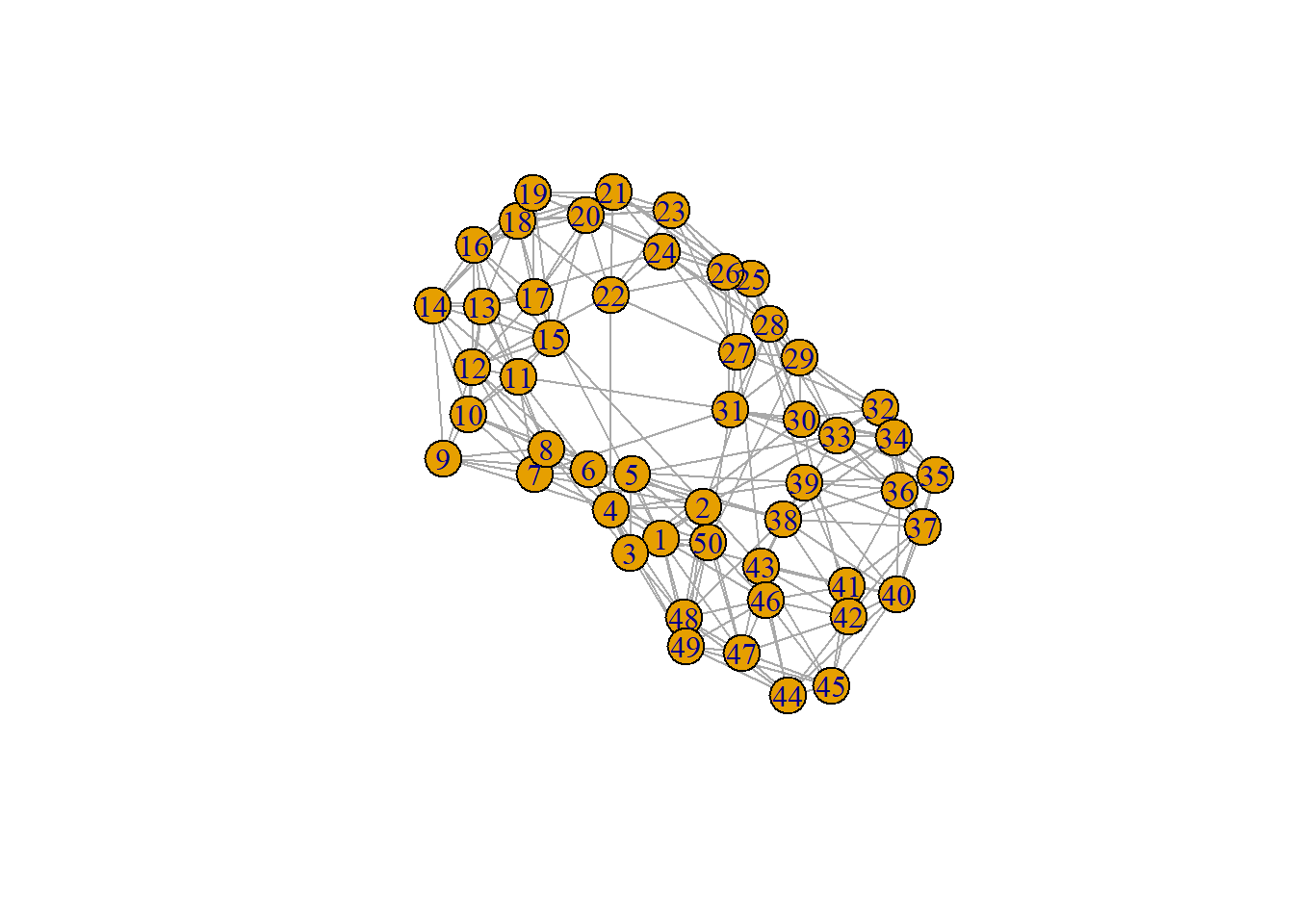

Watts-Strogatz小世界网络是一种特殊的复杂网络模型，由Duncan J. Watts和Steven Strogatz在1998年提出。这种网络模型结合了规则网络和随机网络的特性，具有高集聚系数（节点的邻居之间也有较高的连接概率，形成“团簇”）和短平均路径长度（尽管大部分节点彼此不直接相连，但通过少数几步就可以到达），能够很好地解释许多现实世界中的网络现象，如社交网络的“六度分隔”现象等。

2.2 图论基础

2.2.1 结点的度

度（degree）是指一个结点连接的边的数量。在有向图中，度可以分为入度（in-degree）和出度（out-degree），分别表示指向该结点的边数和从该结点出发的边数。结点的度可以表示为：

2.2.2 路径

对于一个图，我们往往会关心一个结点和另一个结点之间的关系，而要研究两个结点之间的关系，就不得不先知道两个结点之间的路径。路径（path）是指在图中从一个结点到另一个结点的结点序列。路径的长度由路径上的边数决定。如果路径序列中结点不重复出现，那我们称这个路径为简单路径。路径可以帮助分析网络中结点之间的可达性和距离。在计算结点间的路径时，我们有时还会遇到环。环（loop），又称回路，指的是第一个结点和最后一个结点相同的路径。

有时从一个结点到另一个结点的路径可能有很多，但是这些路径之中一定有一个最短路径，即路径上边的权重之和最小的路径。而这个最短路径就是两个结点之间的距离。

Dijkstra算法

Dijkstra算法是荷兰计算机科学家Edsger W. Dijkstra于1956年提出的一种用于计算有权图中最短路径的经典算法。该算法适用于包含非负权重的有向图和无向图。

Dijkstra算法的核心思想是通过贪心策略逐步扩展最近的未处理结点，并更新其邻居结点的距离，直到所有结点的最短路径都确定。具体步骤如下：

  1. 初始化：从起始结点开始，设置起始结点到自身的距离为0，其他结点的距离为无穷大。将所有结点标记为未访问。

  2. 选择结点：从未访问的结点中选择一个距离起始结点最近的结点作为当前结点。

  3. 更新距离：对于当前结点的每个邻居结点，计算从起始结点经过当前结点到达该邻居结点的距离。如果该距离小于当前记录的距离，则更新该邻居结点的距离。

  4. 标记访问：将当前结点标记为已访问。

  5. 重复：重复步骤2到4，直到所有结点都被访问。

在igraph中，我们可以使用shortest_paths计算结点之间的最短路径。注意，要计算最短路径时，我们需要将网络中的边权重视为结点之间的距离，然而这在某些心理学网络的分析中是不合适的。比如，对于一个由偏相关系数矩阵构建的网络，结点A与结点B的边权重很大意味着两个结点的关联很紧密，但是在计算最短路径时二者的距离将视为很远。最短路径往往是在社交网络的分析中使用。

现在我们采用igraph主页的示例生成一个简单的社交网络计算最短路径。

social_network <- make_graph(
  ~ Alice - Boris:Himari:Moshe, Himari - Alice:Nang:Moshe:Samira,
  Ibrahim - Nang:Moshe, Nang - Samira
)
plot(social_network)
shortest_paths(social_network, "Alice", "Nang")
#> $vpath
#> $vpath[[1]]
#> + 3/7 vertices, named, from e41eab2:
#> [1] Alice  Himari Nang  
#> 
#> 
#> $epath
#> NULL
#> 
#> $predecessors
#> NULL
#> 
#> $inbound_edges
#> NULL

我们也可以用distances计算结点之间的距离矩阵。

distances(social_network)
#>         Alice Boris Himari Moshe Nang Samira Ibrahim
#> Alice       0     1      1     1    2      2       2
#> Boris       1     0      2     2    3      3       3
#> Himari      1     2      0     1    1      1       2
#> Moshe       1     2      1     0    2      2       1
#> Nang        2     3      1     2    0      1       1
#> Samira      2     3      1     2    1      0       2
#> Ibrahim     2     3      2     1    1      2       0

2.2.3 连通性

连通性（connectivity）描述了图中结点之间的连接程度。如果图中任意两个结点之间都存在路径我们就称这个图是连通的。连通性可以帮助识别网络中的孤立结点和子图。

一个无向图中的极大连通子图称为连通分量（一个图可有多个）。在有向图中，如果对于每一对结点\(i\)和\(j\)，从\(i\)到\(j\)和从\(j\)到\(i\)都存在路径，则称这个图是强连通图。有向图中的极大强连通子图称为强连通分量。

图的遍历

图的遍历指的是从图中某一结点出发访遍图中其余结点，且使每一个结点被访问且仅被访问一次。图的遍历算法是求解图的连通性问题、拓扑问题等算法的基础。图的遍历通常有两种方法：深度优先搜索（Depth-First Search, DFS）和广度优先搜索（Breadth-First Search, BFS）。

深度优先搜索：从图的指定结点\(v\)出发，先访问结点\(v\)，并将其标记为已访问过，然后依次从\(v\)的未被访问过的邻接结点\(w\)出发进行深度优先搜索，直到图中与\(v\)相连的所有结点都被访问过。如果图中还有未被访问的结点，则从另一未被访问过的结点出发重复上述过程，直到图中所有结点都被访问过为止。

广度优先搜索：从图的指定结点\(v\)出发，先访问结点\(v\)，接着依次访问\(v\)的所有邻结点\(w_1\), \(w_2\), … , \(w_x\)，然后，再依次访问与\(w_1\), \(w_2\), …, \(w_x\) 邻接的所有未被访问过的结点，以此类推，直到所有已访问结点的邻接结点都被访问过为止。如果图中还有未被访问过的结点，则从另一未被访问过的结点出发进行广度优先搜索，直到所有结点都被访问过为止。