4 网络的描述
在构建好网络后,我们就可以对构建好的网络进行描述和分析。首先我们需要对网络进行可视化,也就是将边的列表或权重矩阵转换为图形,在R语言中我们一般使用igraph或者qgraph来进行。对于网络的性质,我们一般可以通过对结点的中心性和网络的拓扑结果进行分析。
4.1 网络可视化
在R语言中对一个网络,例如igraph对象或qgraph对象,可以使用plot函数进行作图。绘制网络。例如,我们可以创建一个20世纪70年代美国一所大学空手道俱乐部34名成员之间的社交网络5。
library(igraph)
#>
#> Attaching package: 'igraph'
#> The following objects are masked from 'package:stats':
#>
#> decompose, spectrum
#> The following object is masked from 'package:base':
#>
#> union
zachary_graph <- make_graph('Zachary')
plot(zachary_graph)
当然,这只是最最简单的可视化方法,为了得到更加美观和有意义的可视化图形,我们可以采用很多方法。
4.1.1 布局算法
图是一个抽象的数学对象,在二维、三维或任何其他几何空间中都没有特定的表示形式。 这就意味着,无论何时我们想将图形可视化,都必须先找到二维或三维空间中顶点到坐标的映射。图论的一个独立分支,即图绘制,试图通过多种图布局算法来解决这个问题。igraph实现了很多布局算法,还能将它们绘制到屏幕上或R本身支持的任何输出格式。
一种常见的布局是把所有结点放在在一个圆环上,可以使用layout_in_circle获得布局,这里得到的是一个N行2列的矩阵,代表了每个结点在二维空间中的坐标。
circle_layout <- layout_in_circle(zachary_graph)
plot(zachary_graph, layout = circle_layout, main = "Zachary Social network with circle layout")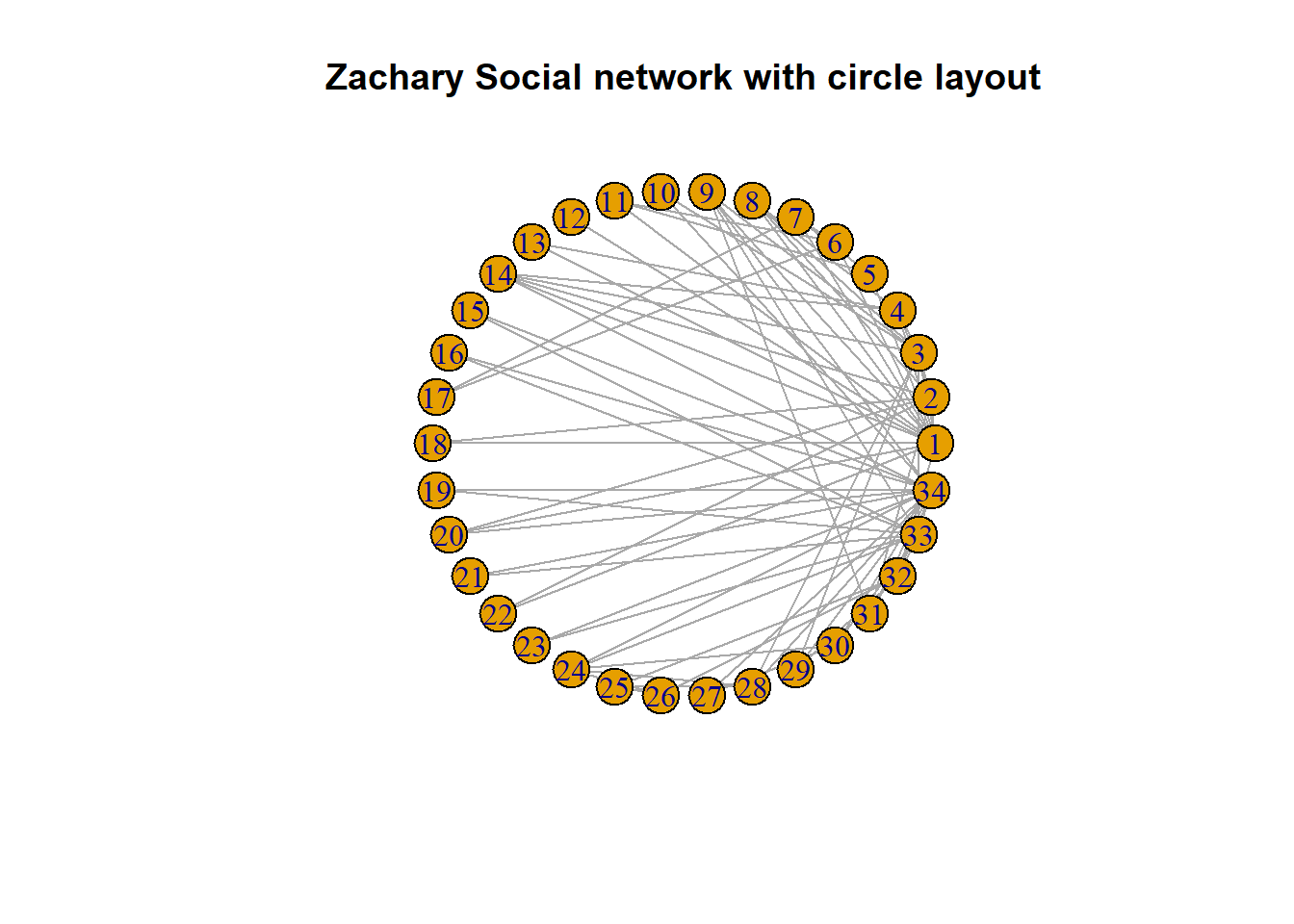
当然,除了直接得到一个单独的布局的矩阵,我们也可以直接在plot中设置layout参数时指定布局算法。例如,我们可以采用Kamada-Kawai算法设计布局。Kamada-Kawai算法是一种用于图布局的力引导算法,旨在将图中的节点在二维或三维空间中进行美观的布局。该算法通过模拟物理系统中的弹簧力并使系统总能量最小化来实现节点的优化排列。如果不指定布局的话,默认采用Fruchterman-Reingold算法,这也是一种常用的力引导布局算法,该算法也基于物理模拟的思想,将结点视为带电粒子,通过斥力和引力的相互作用来调整节点的位置。
plot(zachary_graph, layout = layout_with_kk, main = "Zachary Social network with the Kamada-Kawai layout algorithm")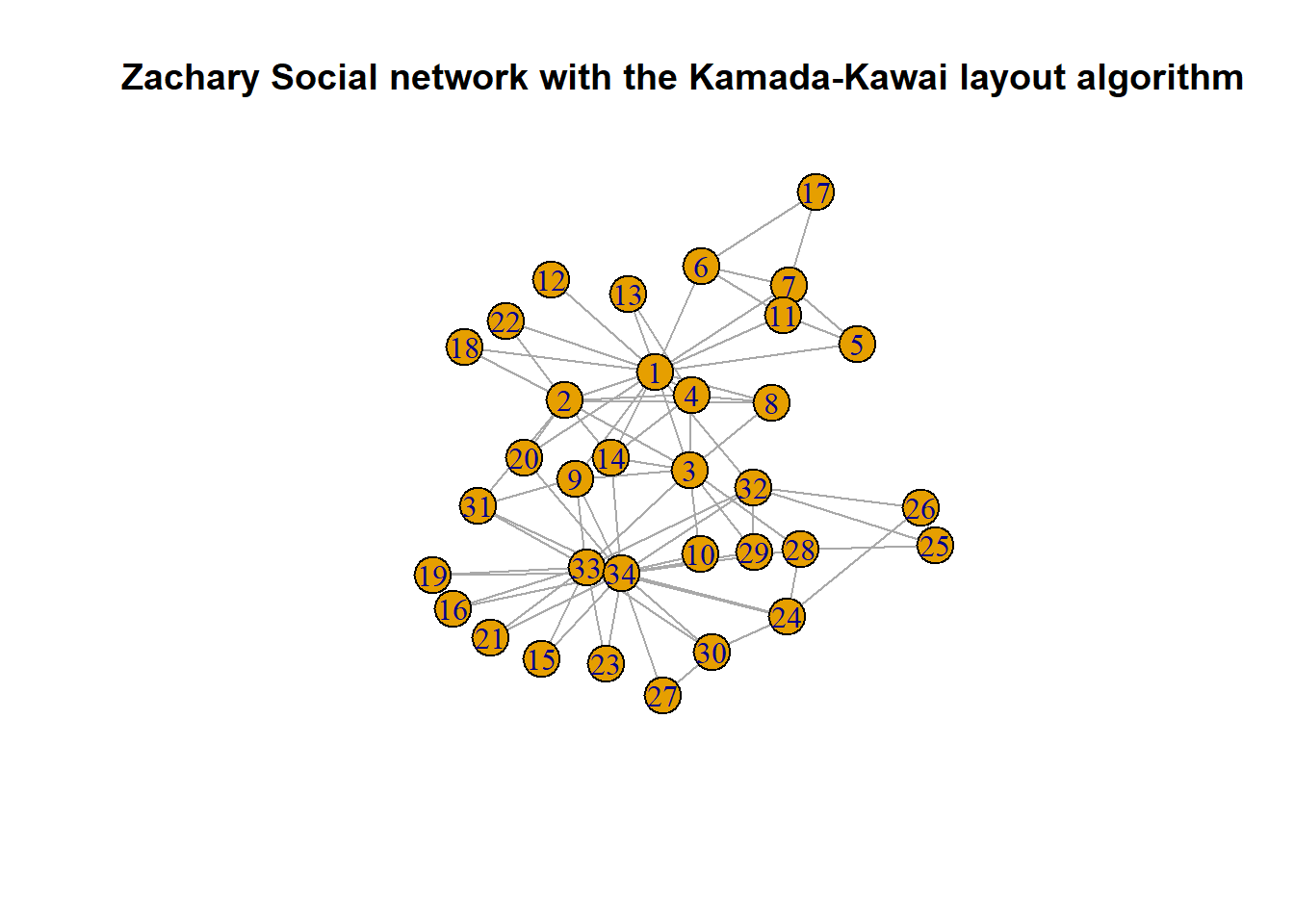
除了这些igraph还提供了多种布局算法,详情可以访问igraph主页的相关介绍 https://r.igraph.org/articles/igraph.html#layout-algorithms。
在qgraph中使用qgraph作图时可以通过设定layout参数指定网络的布局算法。主要有三种布局:“circle”、“groups”和”spring”。“circle”布局中所有结点排列在一个圆环上,“groups”使得每一个组的结点排列在一个圆环,“spring”即Fruchterman-Reingold算法布局(igraph曾经也有一个布局叫”spring”但是现在已经移除)。当然,layout也可以直接传入包含所有结点坐标的矩阵。
library(qgraph)
adj_matrix <- as_adjacency_matrix(zachary_graph) %>%
as.matrix()
qgraph(adj_matrix, layout = "spring")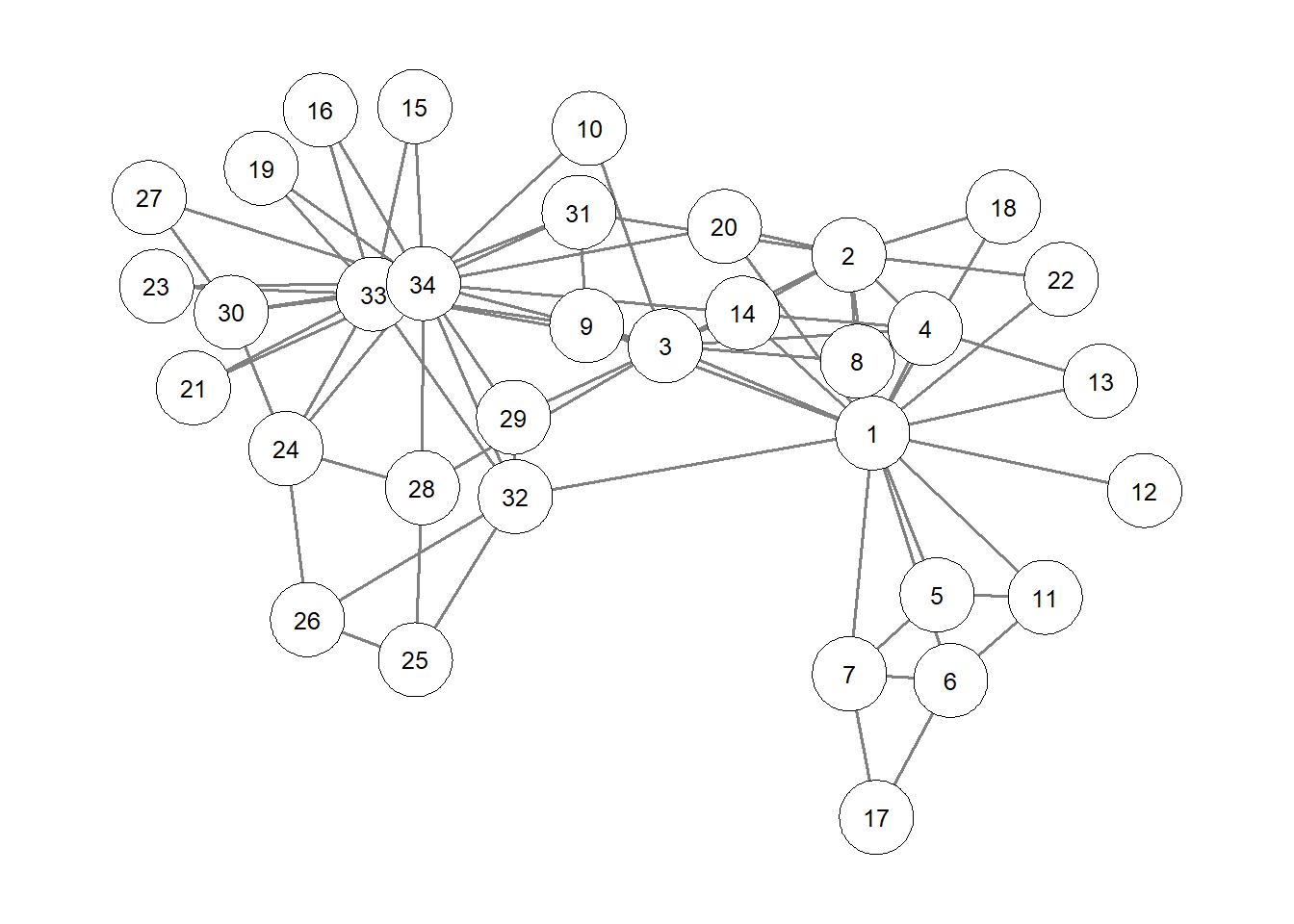
4.2 结点的中心性
结点的中心性(centrality)描述了一个结点和其他结点的关联,是衡量结点在网络中重要性的一类指标。常见的中心性指标包括强度(strength)、度中心性(degree centrality)、接近中心性(closeness centrality)、中介中心性(betweenness centrality)、特征向量中心性(eigenvector centrality)和预期影响(expected influence, EI)。这些指标可以帮助识别网络中的关键结点。这些中心性指标中,有些适用于大多数网络,而有些则只适用于特定的网络,因此在使用时需要格外小心。
4.2.1 结点强度
结点的强度即是某个结点与之相连的边的权重的绝对值之和:
\[ \text{Strength}(i)=\sum_{j=1}^n|w_{ij}| \]
其中,\(w_{ij}\)表示结点\(i\)和结点\(j\)之间的边权重。结点强度表示了变量与网络中其他变量的平均条件关联程度,是经常使用的中心性指标。
在igraph中,我们可以使用strength计算结点的强度。
strength(zachary_graph)
#> [1] 16 9 10 6 3 4 4 4 5 2 3 1 2 5 2 2 2 2
#> [19] 2 3 2 2 2 5 3 3 2 4 3 4 4 6 12 174.2.2 度中心性
度中心性是衡量一个结点在网络中直接连接到其他结点数量的指标。它是最简单、最直观的中心性度量方法。无向图中的度中心性等于该结点的度,即与该节点直接相连的边的数量。有向图中的度中心性可以进一步分为入度中心性和出度中心性。入度中心性表示指向该结点的边的数量,出度中心性表示从该结点出发的边的数量。
在igraph中,我们可以使用degree计算结点的度。
degree(zachary_graph)
#> [1] 16 9 10 6 3 4 4 4 5 2 3 1 2 5 2 2 2 2
#> [19] 2 3 2 2 2 5 3 3 2 4 3 4 4 6 12 174.2.3 接近中心性
接近中心性指的是一个结点到网络中所有其他结点的平均最短路径长度的倒数,衡量了结点与其他结点之间的远近关系。接近中心性高的结点通常位于网络的中心位置,能够更快地与其他结点进行通信。
结点\(v\)接近中心性的计算公式如下:
\[ \text{Closness}(i) = \frac{1}{\sum_{i\neq j}d_{ji}} \]
其中,\(i\)表示图中非\(j\)的结点,\(d_{ji}\)表示结点\(j\)到结点\(i\)的最短路径。
需要注意的是,接近中心性的概念是以距离为基础,最初在社交网络中使用。在心理测量学数据的网络分析中,边权重表示变量间的条件关联,权重越大关联越大,不能认为距离越远,因此接近中心性不一定适用。
在igraph中,我们可以使用closeness计算结点的接近中心性。
closeness(zachary_graph)
#> [1] 0.01724138 0.01470588 0.01694915 0.01408451 0.01149425
#> [6] 0.01162791 0.01162791 0.01333333 0.01562500 0.01315789
#> [11] 0.01149425 0.01111111 0.01123596 0.01562500 0.01123596
#> [16] 0.01123596 0.00862069 0.01136364 0.01123596 0.01515152
#> [21] 0.01123596 0.01136364 0.01123596 0.01190476 0.01136364
#> [26] 0.01136364 0.01098901 0.01388889 0.01369863 0.01162791
#> [31] 0.01388889 0.01639344 0.01562500 0.016666674.2.4 中介中心性
中介中心性衡量一个结点在网络中作为其他结点对之间最短路径的中介程度,通过计算有多少条最短路径通过一个结点来衡量。中介中心性高的结点在网络中起到“桥梁”作用,控制着信息的流动。
结点\(v\)中介中心性的计算公式如下:
\[ \text{Betweenness}(i) = \sum_{i \neq j, i \neq k, j \neq k} \frac{g_{kij}}{g_{jk}} \]
其中,\(g_{jk}\)表示结点\(j\)到结点\(k\)的最短路径的数量,\(g_{kij}\)表示从\(k\)到\(j\)的经过\(i\)的最短路径的数量。
在igraph中,我们可以使用betweenness计算结点的中介中心性。
betweenness(zachary_graph)
#> [1] 231.0714286 28.4785714 75.8507937 6.2880952
#> [5] 0.3333333 15.8333333 15.8333333 0.0000000
#> [9] 29.5293651 0.4476190 0.3333333 0.0000000
#> [13] 0.0000000 24.2158730 0.0000000 0.0000000
#> [17] 0.0000000 0.0000000 0.0000000 17.1468254
#> [21] 0.0000000 0.0000000 0.0000000 9.3000000
#> [25] 1.1666667 2.0277778 0.0000000 11.7920635
#> [29] 0.9476190 1.5428571 7.6095238 73.0095238
#> [33] 76.6904762 160.55158734.2.5 特征向量中心性
特征向量中心性是一种衡量网络中结点重要性的方法。它不仅考虑结点的直接连接数量,还考虑这些连接结点本身的重要性。换句话说,一个结点的中心性不仅取决于它有多少邻居结点,还取决于这些邻居结点的中心性。
特征向量中心性可以通过计算邻接矩阵的主特征向量来获得。在igraph中,我们可以使用eigen_centrality计算结点的中介中心性。
eigen_centrality(zachary_graph)$vector
#> [1] 0.95213237 0.71233514 0.84955420 0.56561431 0.20347148
#> [6] 0.21288383 0.21288383 0.45789093 0.60906844 0.27499812
#> [11] 0.20347148 0.14156633 0.22566382 0.60657439 0.27159396
#> [16] 0.27159396 0.06330461 0.24747879 0.27159396 0.39616224
#> [21] 0.27159396 0.24747879 0.27159396 0.40207086 0.15280670
#> [26] 0.15857597 0.20242852 0.35749923 0.35107297 0.36147301
#> [31] 0.46806481 0.51165649 0.82665886 1.000000004.2.6 预期影响
预期影响是一个考虑了网络中正负边权重的中心性指标,在含有负权重边的网络中优于传统中心性指标。当变量具有非任意性编码时,例如所有变量的值越高都表示更严重的症状时,这种方法可能比较合适。
预期影响将连接到一个结点的边的权值相加,而不取绝对值:
\[ \text{ExpectedInfluence}(i)=\sum_{j=1}^na_{ij}w_{ij} \]
\(a_{ij}\)表示结点\(i\)和\(j\)是否直接相连。
预期影响可以使用qgraph中的centrality计算。qgraph中还可以使用centrality_plot绘制中心性指标的图:
zachary_qgraph <- qgraph(as.matrix(as_adjacency_matrix(zachary_graph)))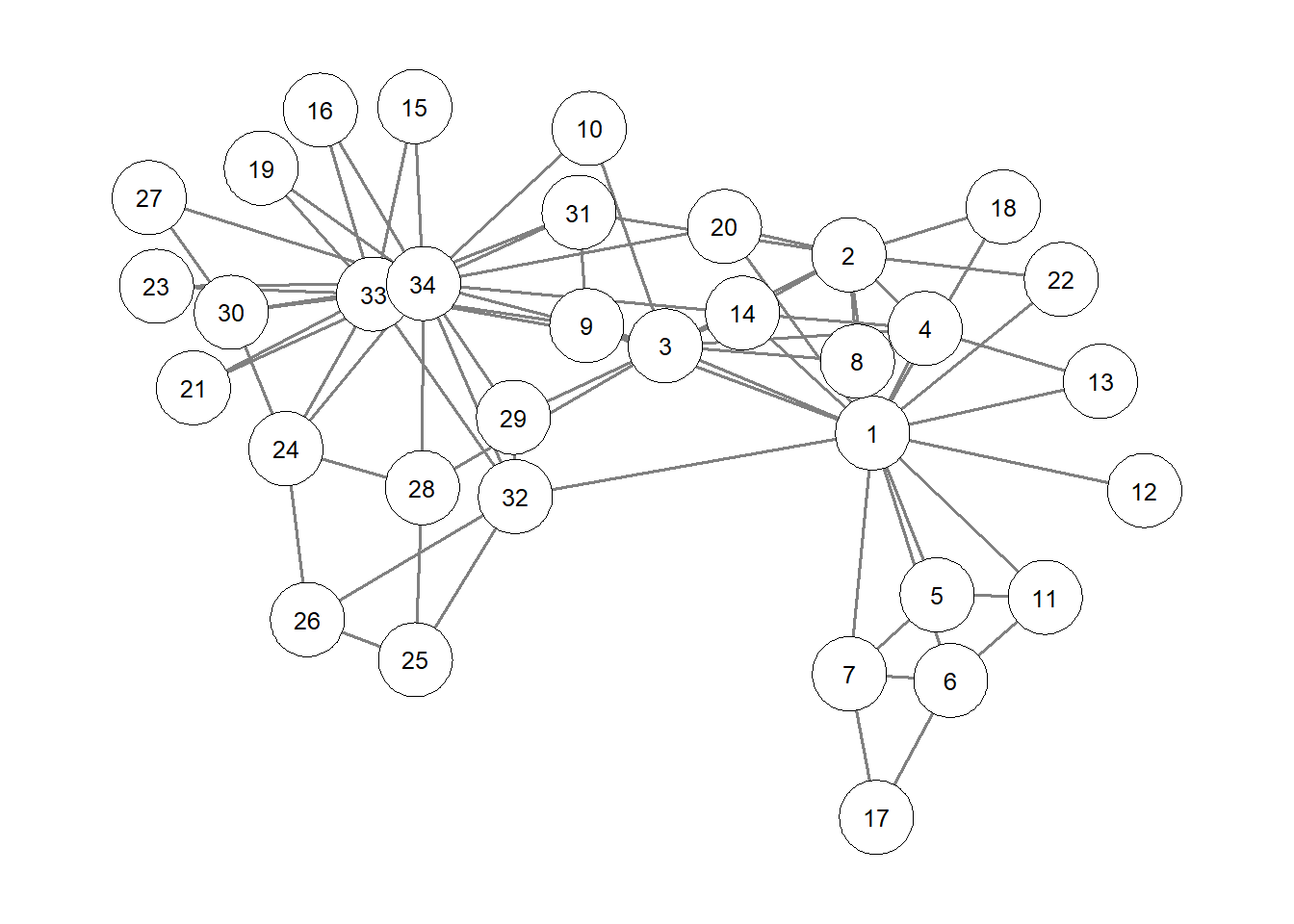
centrality(zachary_qgraph)$InExpectedInfluence
#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
#> 16 9 10 6 3 4 4 4 5 2 3 1 2 5 2 2 2 2 2 3
#> 21 22 23 24 25 26 27 28 29 30 31 32 33 34
#> 2 2 2 5 3 3 2 4 3 4 4 6 12 17
centralityPlot(zachary_qgraph, include = "all")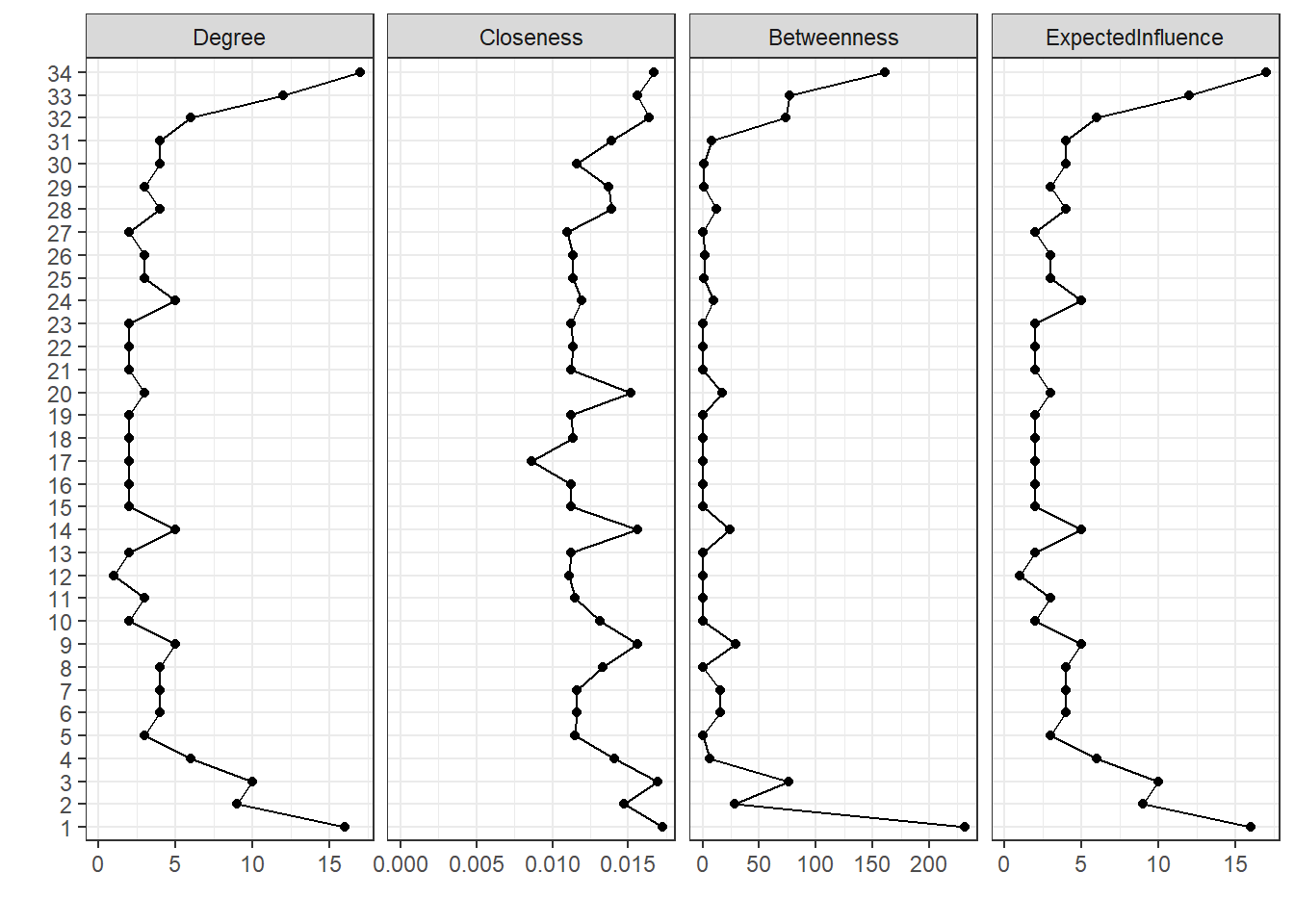
在这个例子里面,度和预期影响是相同的,因为这是一个无权图。
预期影响最初在这篇文献中提出:
Robinaugh, D. J., Millner, A. J., & McNally, R. J. (2016). Identifying highly influential nodes in the complicated grief network. Journal of abnormal psychology, 125(6), 747–757. https://doi.org/10.1037/abn0000181
4.3 网络的拓扑性质
除了量化网络的局部属性的度量之外,还有几个度量可以将网络架构作为一个整体来量化,称为全局网络属性。这种体系结构有时被称为网络的拓扑结构:网络中的结点和边的组织。了解网络的体系结构可以传递关于信息或活动在系统中传播的速度的信息。
4.3.1 连通性
连通性(connectivity)描述了图中结点之间的连接程度。如果图中任意两个结点之间都存在路径我们就称这个图是连通的。连通性可以帮助识别网络中的孤立结点和子图。
一个无向图中的极大连通子图称为连通分量(一个图可有多个)。在有向图中,如果对于每一对结点\(i\)和\(j\),从\(i\)到\(j\)和从\(j\)到\(i\)都存在路径,则称这个图是强连通图。有向图中的极大强连通子图称为强连通分量。
在igraph中,我们也可以计算图的连通性和连通分量。我们可以首先生成一个随机的图。
adjacent_matrix <- matrix(sample(0:1, 100, replace = TRUE, prob = c(0.9, 0.1)), ncol = 10)
g <- graph_from_adjacency_matrix(adjacent_matrix)
plot(g)
这个图显然是不连通的。我们可以用is_connected检查一个图是否连通。
is_connected(g)
#> [1] FALSE我们可以用components计算连通分量。
components(g)
#> $membership
#> [1] 1 2 3 2 1 1 1 1 4 1
#>
#> $csize
#> [1] 6 2 1 1
#>
#> $no
#> [1] 44.3.2 聚类系数
传递性(transitivity)又称聚类系数(clustering coefficient), 测量的是一个结点的相邻顶点结点的概率。聚类系数包括两类:结点水平的局部聚类系数和网络水平的全局聚类系数。对于有权图的聚类系数有几种描述,这里我们使用A. Barrat的定义6,这是一个结点水平的局部聚类系数,其公式为
\[ C_i^w = \frac{1}{s_i(k_i-1)}\sum_{j,h}\frac{w_{ij}+w_{ih}}{2}a_{ij}a_{ih}a_{jh} \]
其中,\(s_i\)指结点\(i\)的强度(该结点相连边权重之和),\(a_{ij}\)是邻接矩阵中的元素,\(k_i\)指结点\(i\)的度,\(w_{ij}\)为边权重。
在igraph中可以使用transitivity计算。以一个随机生成的小世界网络为例。
g <- sample_smallworld(1, 50, 5, 0.05)
transitivity(g)
#> [1] 0.52225654.3.3 小世界性质
Duncan J. Watts和Steven Strogatz(1998)指出,许多网络具有介于随机网络和有组织网络之间的属性:网络是整体有组织的,但可能包括一些随机连接。这导致了一个平均最短路径(APL,整个网络中所有结点对之间的最短路径长度的平均值)都低和全局聚类都高的网络结构,这被称为小世界网络(small-world)。“小世界”是以六度分离现象命名的;所有人彼此之间平均只有六个社会联系。
要量化一个网络\(G\)的小世界性质,我们可以把这个网络的APL和传递性与拥有同样结点个数的随机网络\(G_R\)的相应性质进行比较。一般来说小世界网络的APL与随机网络相似:
\[ \text{APL}(G)\approx\text{APL}(G_R) \]
而小世界网络的聚类性质比随机网络要高:
\[ \text{Transitivity}(G)\gg\text{Transitivity}(G_R) \]
一种计算小世界性质的方式是:
\[ \text{SmallWorld}(G)=\frac{\text{Transitivity}(G)/\text{Transitivity}(G_R)}{\text{APL}(G)/\text{APL}(G_R)} \]
在qgraph中可以使用smallworldness计算小世界指标,该函数使用Humphries和Gurney(2008)的算法计算。
smallworldness(g)
#> smallworldness trans_target
#> 2.5561499 0.5222565
#> averagelength_target trans_rnd_M
#> 2.1951020 0.1743358
#> trans_rnd_lo trans_rnd_up
#> 0.1467541 0.2022984
#> averagelength_rnd_M averagelength_rnd_lo
#> 1.8730261 1.8538776
#> averagelength_rnd_up
#> 1.8955143参考文献:Humphries, M. D., & Gurney, K. (2008). Network “small-world-ness”: a quantitative method for determining canonical network equivalence. PLoS One, 3(4), e0002051. https://doi.org/10.1371/journal.pone.0002051