3 网络的构建

心理学研究中的网络分析常常作为一种多变量分析的方法，特别是分析心理测量学数据，因此也称为心理测量学网络分析（psychometric network analysis）。本章节介绍的网络构建方法就是基于心理测量学数据，其他类型的网络（如社交网络、因果关系网络等）不在本章讨论范围之内。

3.1 构建网络的数据

本章中讨论的心理测量学数据，一般指的是量表项目的作答、症状评分和认知测试得分等等，有时可能还包括背景变量（如年龄和性别、遗传信息、生理标记、医疗条件、实验干预等），这些变量在网络中就是结点。基于我们所关心的研究问题，我们收集到的数据一般包括横断面数据、时间序列数据和面板设计。

横断面数据（cross-sectional data）：在横断面数据中，网络是大样本（T = 1，N很大）中单一时间点测量的变量之间条件关联的描述。在这种情况下，变量之间的关联是由个体差异驱动的，这使得此类网络在研究心理测验的心理测量学结构时非常有用。
时间序列数据（time-series data）：在时间序列数据中，网络描述了个体（T很大，N ≥ 1）的变量时间序列之间的多变量依赖关系。此类网络最常应用于需要深入了解系统动态结构的情景。
面板数据（panel data）：在面板数据（也称为纵向数据）的中，一组有限的重复测量既能描述给定时间点变量的关联结构，也能描述这些条件依赖关系随时间（N > T）变化的方式。这种测量方法可以同时揭示个体差异和个体内部变化的结构。

3.2 PMRF

大多数网络构建方法使用条件关联（conditional association）来定义变量中的网络结构。当两个变量之间存在概率依赖关系时，这两个变量之间的条件关联就成立，而条件就是数据中的所有其他变量。使用哪种条件关联的度量取决于数据的结构，例如，对于多元正态数据可以使用偏相关（partial correlation），而对于二分数据可以使用逻辑回归系数（logistic regression coefficient）。这种条件关联在网络中通常描述为两个结点之间的边权重。如果两个变量之间的关联可以用网络中的其他变量来解释，则当这些其他变量被控制时，它们之间的条件关联就会消失，那么相应的结点就会在网络中无直接连接。

在构建网络时，我们经常采用配对马尔科夫随机场（Pairwise Markov Random Field , PMRF）来描述多变量的联合概率分布。RMRF实际上是一种无向图模型，以结点表示变量、以边表示变量间的条件关联。

PMRF应用十分广泛，可以作为统计模型的框架，也可以作为预测模型或从中发现潜在的因果关系。

PMRF由很多种类型。如果数据是连续的，一种常用的PMRF是高斯图模型（Gaussian Graphical Model, GGM），其中边的权重为偏相关系数（partial correlation coefficient），因此高斯图模型的实质就是一个偏相关系数矩阵。如果数据是二分的，则可以使用Ising模型，其中边的权重为对数线性关系。Ising模型和高斯图模型可以结合到混合图模型中，在混合图模型中，边被表示为为广义线性模型的回归系数。混合图模型代表了PMRF估计的最一般方法，也允许包含分类变量和计数变量。

3.2.1 高斯图模型

高斯图模型（Gaussian Graphical Model, GGM）是一种常见的应用于连续型变量的PMRF，其实质是一个偏相关稀疏矩阵，因此也叫偏相关系数网络。

设\(\boldsymbol{Y}\)为表示一个被试的\(n\)个反应变量的向量，我们假设\(\boldsymbol{Y}\)服从均值向量为\(\boldsymbol{\mu}\)、协方差矩阵为\(\boldsymbol{\Sigma}\)的正态分布：

\[ \boldsymbol{Y}\sim N(\boldsymbol{\mu},\boldsymbol{\Sigma}) \]

在高斯图模型中，我们关心协方差矩阵的逆\(\boldsymbol{K}\)，也叫精确矩阵（precision matrix）：

\[ \boldsymbol{K}=\boldsymbol{\Sigma}^{-1} \]

精确矩阵可以转换为偏相关系数：

\[ \omega_{ij}=-\frac{\kappa_{ij}}{\sqrt{\kappa_{ii}\kappa_{jj}}}\ \ \text{if}\ i\neq j \]

在bootnet包中，我们可以用estimateNetwork函数来估计一个高斯图模型，即得到一个偏相关系数网络。我们使用psych包中的大五人格数据bfi，我们只取前25个量表的数据。

library(bootnet)
#> Loading required package: ggplot2
#> This is bootnet 1.6
#> For questions and issues, please see github.com/SachaEpskamp/bootnet.
library(psych)
#> 
#> Attaching package: 'psych'
#> The following objects are masked from 'package:ggplot2':
#> 
#>     %+%, alpha
data(bfi)
bfi <- bfi[,1:25]
network <- estimateNetwork(bfi, default = "pcor")
#> Estimating Network. Using package::function:
#>   - qgraph::qgraph(..., graph = 'pcor') for network computation
#>   - psych::corr.p for significance thresholding

我们可以根据偏相关系数的显著性进行边的选择，设置threshold = "sig"，阈值\(\alpha\)设为0.05。

network <- estimateNetwork(bfi, default = "pcor", threshold = "sig", alpha = 0.05)
#> Estimating Network. Using package::function:
#>   - qgraph::qgraph(..., graph = 'pcor') for network computation
#>   - psych::corr.p for significance thresholding
plot(network)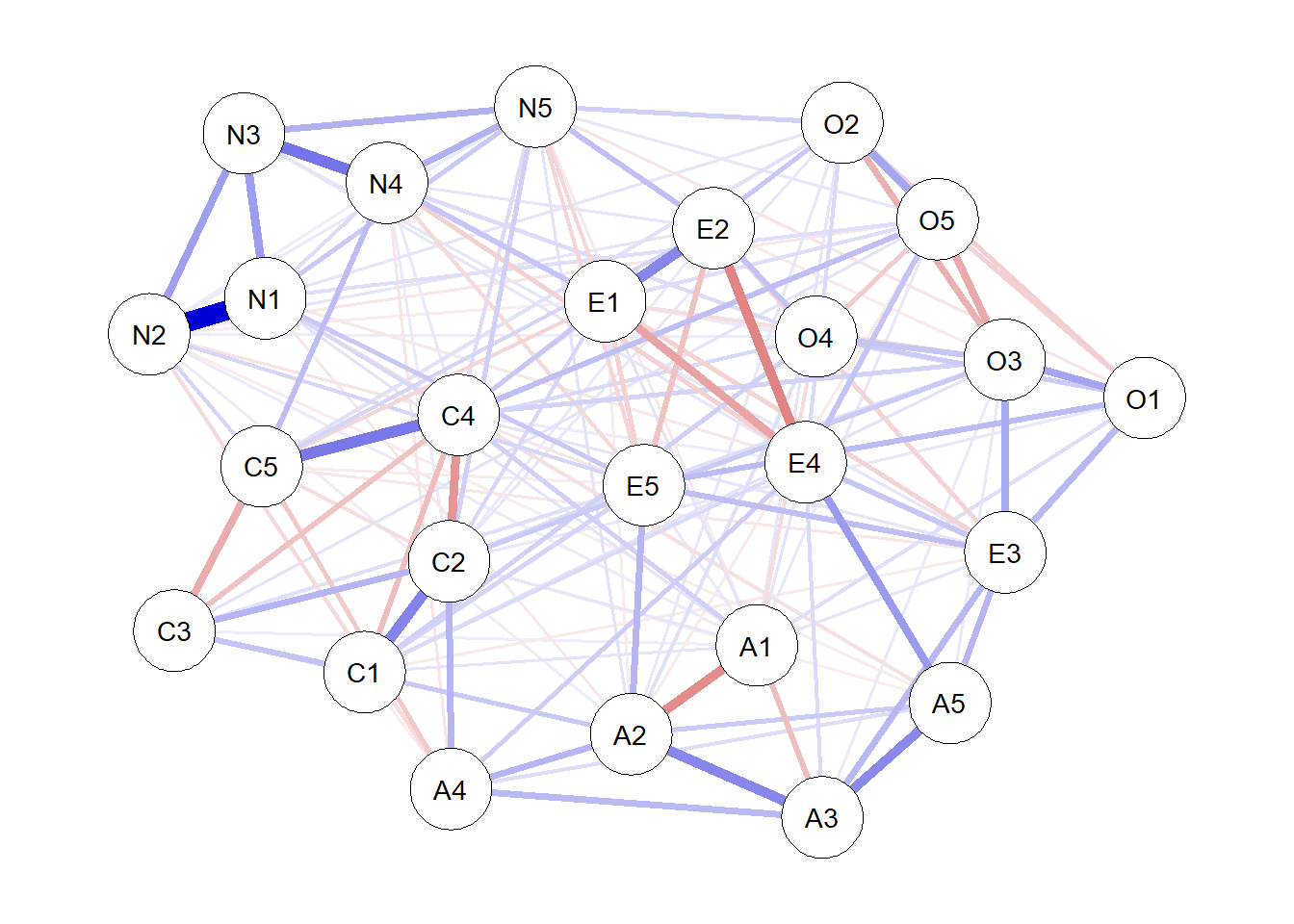

3.2.1.1 Graphical LASSO

如刚才建立的网络所示，各个结点之间的边多而繁杂，有时会对分析造成困扰。这个时候我们就需要考虑模型选择（model selection）：如何确定哪些边应该被包含在内，哪些边可以被省略。刚才我们根据偏相关系数的显著性设定阈值进行了选择，下面我们将介绍另外一种模型选择方法——正则化（regularization）。正则化涉及到通过惩罚最大似然估计来估计边权值，具体而言就是在估计模型参数时，模型的拟合会受到模型中参数的复杂性的惩罚（例如，网络中包含了多少条边）。经常应用于PMRF的正则化是“图像最小绝对值收敛和选择算法” （graphical Least Absolute Shrinkage and Selection Operator, graphical LASSO）。graphical LASSO以一个协方差矩阵或相关矩阵作为输入，并使用正则化的多元估计来估计GGM。惩罚的大小通过一个调谐参数\(\lambda\)确定，\(\lambda\)为0表示没有惩罚。

正则化与LASSO的原理

在正则化中，参数通过优化经过惩罚的似然函数（penalized likelihood function）进行估计。令\(L(\boldsymbol{D};\boldsymbol{\theta})\)为数据\(\boldsymbol{D}\)在给定参数\(\boldsymbol{\theta}\)下的对数似然函数。一般而言，参数的最大似然估计为：

\[ \boldsymbol{\hat{\theta}}=\text{argmax}_\theta(L(\boldsymbol{D};\boldsymbol{\theta})) \]

在正则化中，一个惩罚项被添加到表达式中：

\[ \boldsymbol{\hat{\theta}}=\text{argmax}_\theta(L(\boldsymbol{D};\boldsymbol{\theta})-\lambda \text{Penalty}(\boldsymbol{\theta})) \]

在LASSO中，惩罚项为：

\[ \text{Penalty}_{\text{LASSO}}(\boldsymbol{\theta})=\sum_{i\in S}|\theta_i| \]

其中，\(S\)为受到惩罚的参数的集合。

关于Graphical LASSO可以参考文献Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9(3), 432–441. https://doi.org/10.1093/biostatistics/kxm045

在R语言中，glasso包为我们提供了使用Graphical LASSO进行网络估计的函数。

3.2.1.2 EBICglasso

在R语言中，目前最常用的一种Graphical LASSO算法是qgraph包中的EBICglasso，这种算法将Graphical LASSO和扩展贝叶斯信息准则（Extended Bayesian Information Criterion, EBIC）结合，它在网络分析特别是在处理高维数据时非常有效。算法中EBIC用于选择最佳的调谐参数，平衡模型的拟合优度和复杂度。EBIC在传统BIC的基础上增加了一个调节项，以更好地处理高维数据。

qgraph包是R语言中用于绘制和分析加权网络的强大工具。它最初由Sacha Epskamp³ 等人开发，旨在提供灵活且高效的网络可视化方法，特别适用于心理测量数据的可视化和图形模型的估计。在qgraph中，我们首先使用cor_auto计算数据的相关系数矩阵。cor_auto函数主要用于自动计算适当的相关系数矩阵。它是一个围绕lavaan包中lavCor函数的封装，能够基于多种相关性（如多序列相关、序列相关和皮尔逊相关）计算相关系数矩阵。cor_auto可以自动检测有序变量，并检测相关系数矩阵是否正定⁴。

library(qgraph)
bfi_data <- na.omit(bfi)
correlation <- cor_auto(bfi_data, detectOrdinal = FALSE)

然后，我们可以使用EBICglasso函数估计GGM。EBICglasso接受传入一个相关系数矩阵或协方差矩阵，传出结果为一个偏相关系数矩阵。函数中有一个EBIC的参数gamma，默认为0.5，取0时将采用传统的BIC选择参数。

EBICglasso_result <- EBICglasso(correlation, n = nrow(bfi_data), gamma = 0.5)
#> Warning in EBICglassoCore(S = S, n = n, gamma = gamma,
#> penalize.diagonal = penalize.diagonal, : A dense
#> regularized network was selected (lambda < 0.1 *
#> lambda.max). Recent work indicates a possible drop in
#> specificity. Interpret the presence of the smallest edges
#> with care. Setting threshold = TRUE will enforce higher
#> specificity, at the cost of sensitivity.

对于得到的偏相关系数矩阵，也就是GGM，我们可以使用qgraph函数构建网络并进行可视化。qgraph接受传入的数据类型可以是一个权重矩阵（如偏相关系数矩阵）或者一个边列表，也可以是使用sem包得到的sem类型、lavaan包得到的lavaan类型等其他类型的对象。qgraph能够构建网络返回一个qgraph对象，同时把结果传递给绘图函数绘制图像。

network <- qgraph(EBICglasso_result, 
                  layout = "spring", parallelEdge = TRUE, 
                  cut = 0, theme = "colorblind")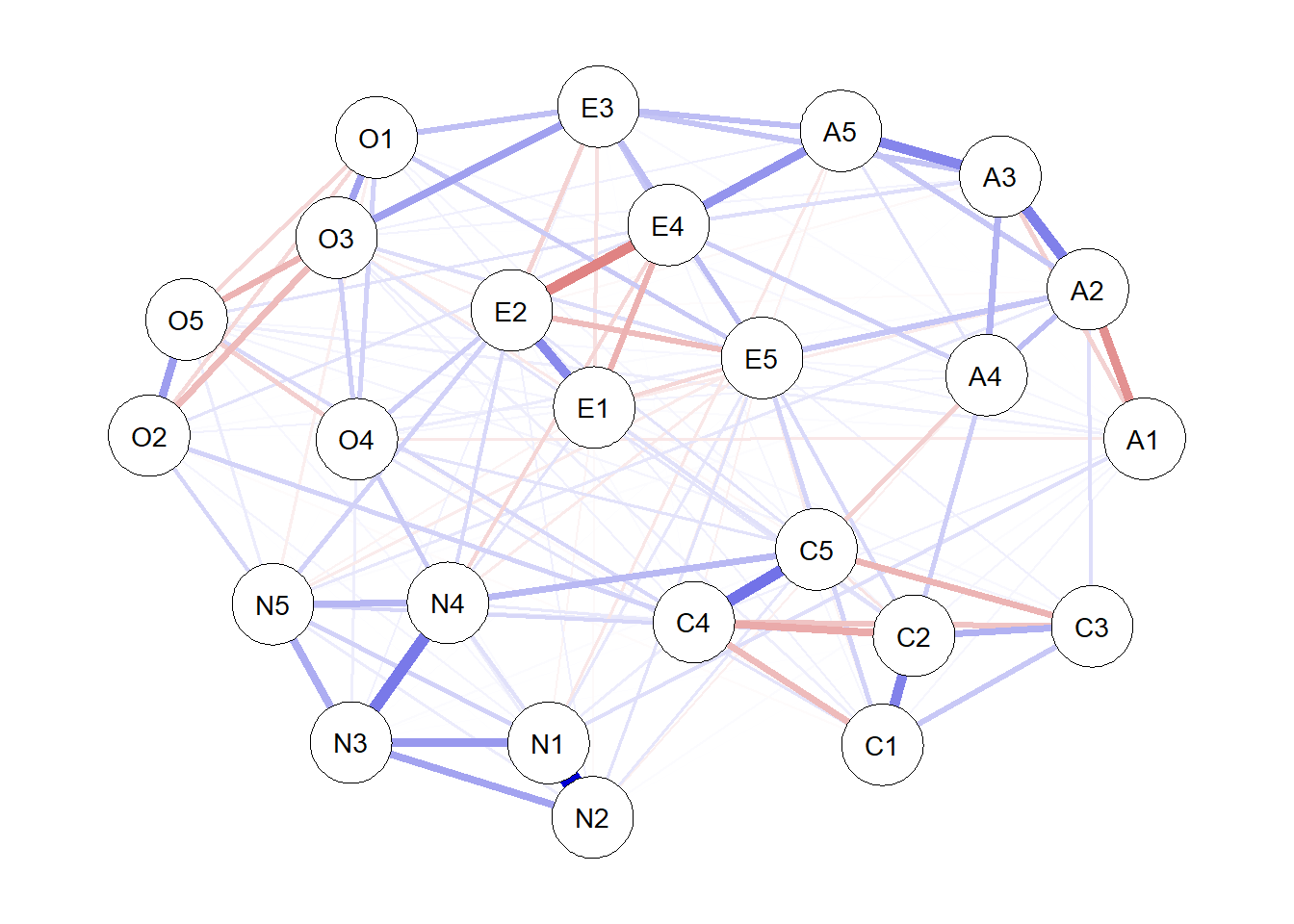

3.2.2 Ising模型

Ising模型是用于估计二分变量的联合概率分布的网络估计方法。Ising模型最初是由物理学家Ernst Ising在1925年提出，用于研究磁性材料中的自旋相互作用，后来被用到网络分析领域。Ising模型中的每个结点（或变量）都有一个自旋，通常表示为+1和-1（或0和1）。在进行参数估计时，Ising模型采用逻辑斯蒂回归计算结点之间的相关关系。

Ising模型可以表示为：

\[ P(\boldsymbol{Y}=\boldsymbol{y})=\frac{\exp(\sum_Iy_i\tau_i+\sum_{<i,j>}y_iy_j\omega_{ij})}{\sum_y\exp(\sum_iy_i\tau_i+\sum_{<i,j>}y_iy_j\omega_{ij})} \]

其中\(\boldsymbol{Y}\)为一个被试的二分类反应变量的向量，参数\(\tau_i\)为一个阈值，\(\omega_{ij}\)为网络参数，表示变量\(i\)和变量\(j\)之间关联的强度。

在R语言中，我们可以使用IsingSampler和IsingFit两个包来进行Ising模型的采样（模拟数据）和拟合。

首先我们可以在igraph中创建一个小世界网络，并为各个边赋予权重，然后使这个权重矩阵为对角矩阵。

library(igraph)
#> 
#> Attaching package: 'igraph'
#> The following objects are masked from 'package:stats':
#> 
#>     decompose, spectrum
#> The following object is masked from 'package:base':
#> 
#>     union
library(IsingSampler)
#> Loading required package: Rcpp
library(IsingFit)
set.seed(2024)

n_nodes <- 8
smallworld_network <- sample_smallworld(dim = 1, 
                                        size = n_nodes, nei = 1, p = 0.2) %>%
  as_adjacency_matrix() %>%
  as.matrix() %>%
  apply(c(1,2),function(x) x * rnorm(1, mean = 1, sd = 0.3))
smallworld_network[lower.tri(smallworld_network)] <- t(smallworld_network)[lower.tri(smallworld_network)]

qgraph(smallworld_network, layout = "spring")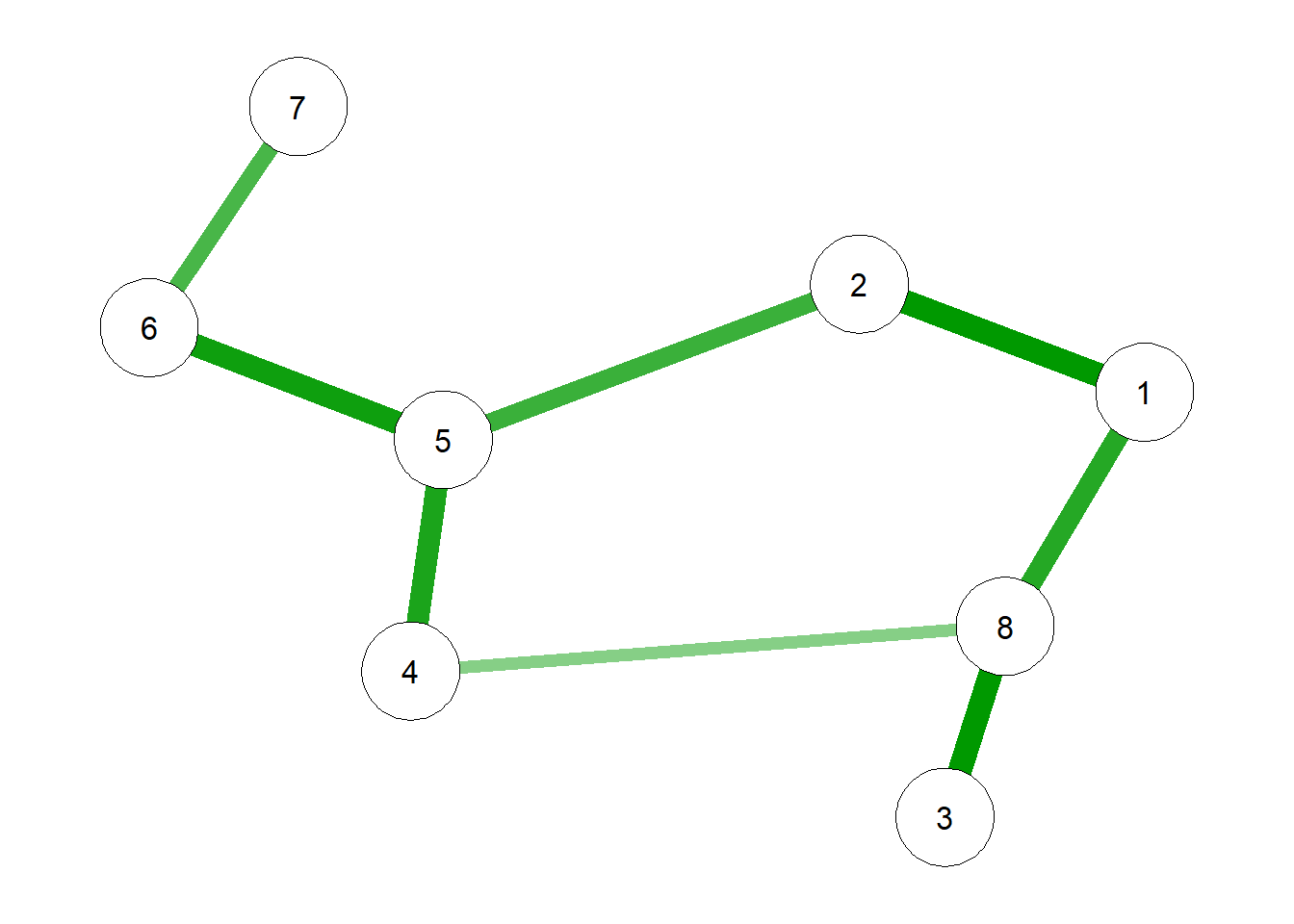

随后我们使用IsingSampler进行采样模拟数据

sample <- IsingSampler(n = 1000, 
                     graph = smallworld_network,
                     thresholds = rep(0,nrow(smallworld_network)), 
                     beta = 1,
                     responses = c(0L, 1L))

得到数据后，我们可以使用IsingFit包中的IsingFit函数拟合模型。IsingFit使用eLASSO算法拟合参数。eLASSO是一种用于二分数据的估计法，结合了伪似然估计和LASSO。

sample_fit <- IsingFit(sample, gamma = 0.5, AND = TRUE)
#> 
  |                                                        
  |                                                  |   0%
  |                                                        
  |======                                            |  12%
  |                                                        
  |============                                      |  25%
  |                                                        
  |===================                               |  38%
  |                                                        
  |=========================                         |  50%
  |                                                        
  |===============================                   |  62%
  |                                                        
  |======================================            |  75%
  |                                                        
  |============================================      |  88%
  |                                                        
  |==================================================| 100%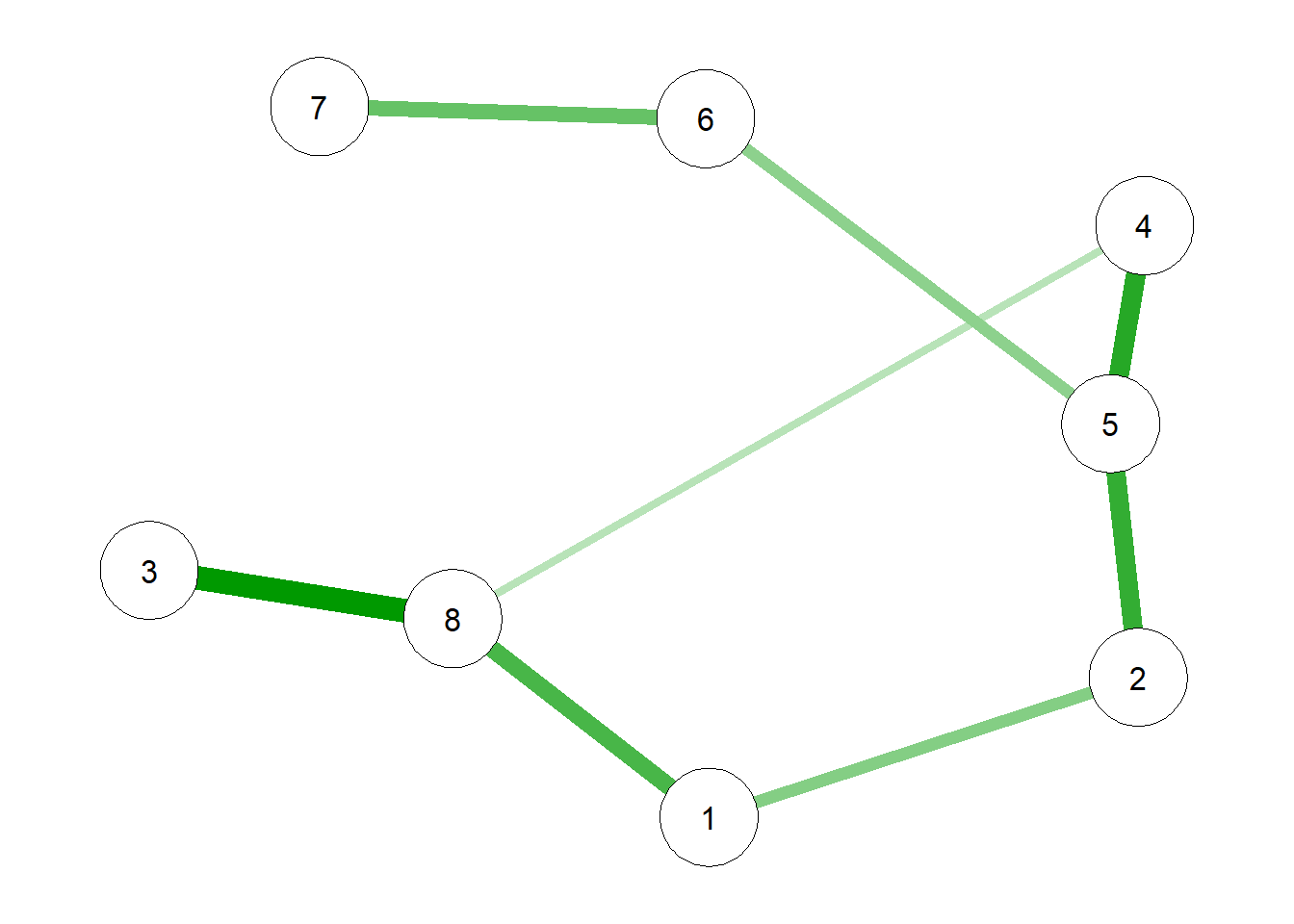

关于Ising模型和eLASSO可以参考文献van Borkulo, C. D., Borsboom, D., Epskamp, S., Blanken, T. F., Boschloo, L., Schoevers, R. A., & Waldorp, L. J. (2014). A new method for constructing networks from binary data. Scientific Reports, 4(1), 5918. https://doi.org/10.1038/srep05918

Finnemann, A., Borsboom, D., Epskamp, S., & van der Maas, H. L. J. (2021). The Theoretical and Statistical Ising Model: A Practical Guide in R. Psych, 3(4), Article 4. https://doi.org/10.3390/psych3040039

3.2.3 混合图模型

3.3 向量自回归模型

3.4 参考文献

Borsboom, D., Deserno, M. K., Rhemtulla, M., Epskamp, S., Fried, E. I., McNally, R. J., Robinaugh, D. J., Perugini, M., Dalege, J., Costantini, G., Isvoranu, A.-M., Wysocki, A. C., van Borkulo, C. D., van Bork, R., & Waldorp, L. J. (2021). Network analysis of multivariate data in psychological science. Nature Reviews Methods Primers, 1(1), 1–18. https://doi.org/10.1038/s43586-021-00055-w
Epskamp, S., Waldorp, L. J., Mõttus, R., & Borsboom, D. (2018). The Gaussian Graphical Model in Cross-Sectional and Time-Series Data. Multivariate Behavioral Research, 53(4), 453–480. https://doi.org/10.1080/00273171.2018.1454823
Isvoranu, A.-M., Epskamp, S., Waldorp, L., & Borsboom, D. (Eds.). (2022). Network Psychometrics with R: A Guide for Behavioral and Social Scientists (1st ed.). Routledge. https://doi.org/10.4324/9781003111238

2 基本概念与图论基础

4 网络的描述